Understanding Quadratic Equations:
Posted 2024-08-30 06:49:57
0
10K
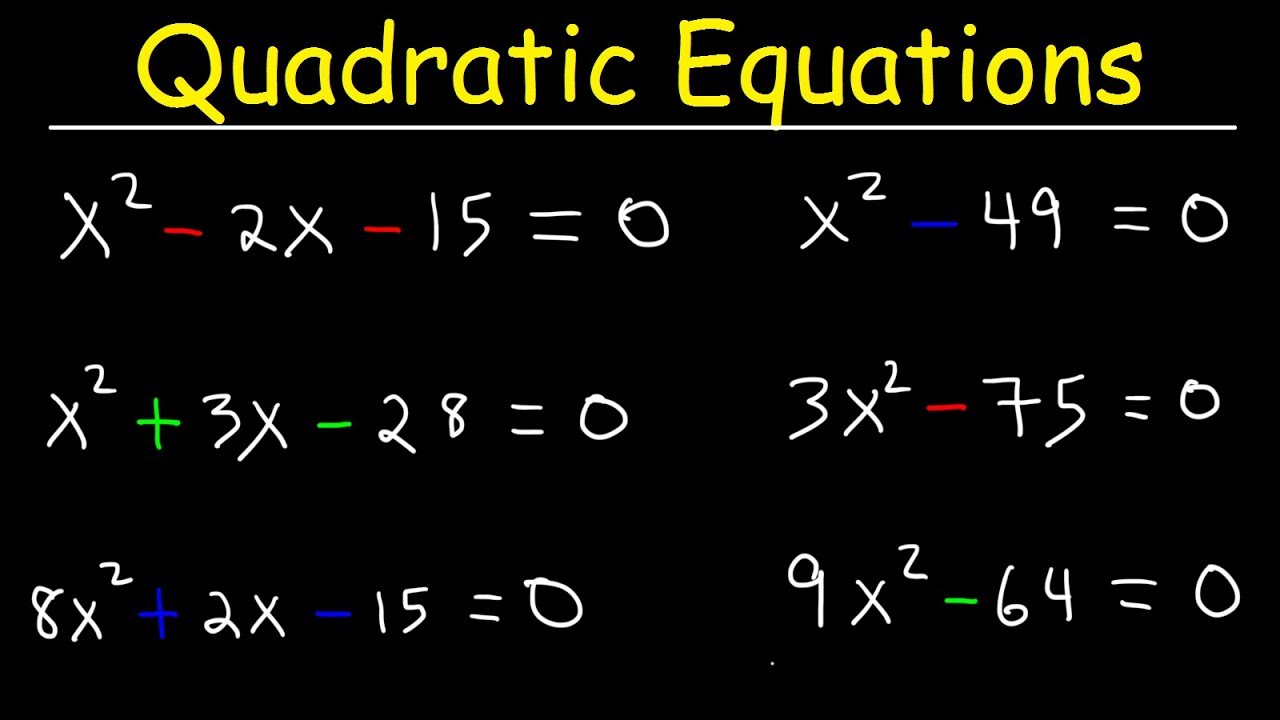
- A quadratic equation is a polynomial equation of degree 2. It can be expressed in the general form:
where a, b, and c are constants, and a ≠ 0.
ax² + bx + c = 0
Methods for Solving Quadratic Equations:
-
Factoring:
- Factor the quadratic expression into two linear factors.
- Set each factor equal to zero and solve for x.
- Example:
x² - 5x + 6 = 0 (x - 2)(x - 3) = 0 x = 2 or x = 3
-
Completing the Square:
- Convert the quadratic equation into a perfect square trinomial.
- Take the square root of both sides and solve for x.
- Example:
x² - 6x + 2 = 0 x² - 6x + 9 = 7 (x - 3)² = 7 x - 3 = ±√7 x = 3 ± √7
-
Quadratic Formula:
- Apply the quadratic formula:
x = (-b ± √(b² - 4ac)) / (2a) - Substitute the values of a, b, and c from the quadratic equation.
- Simplify and solve for x.
- Apply the quadratic formula:
Example:
Solve the equation: 2x² - 3x - 5 = 0
Method 1: Factoring
- We cannot factor this equation into two linear factors.
Method 2: Completing the Square
- Divide the equation by 2 to simplify:
x² - (3/2)x - (5/2) = 0 - Add (3/4)² to both sides to complete the square:
x² - (3/2)x + (9/16) = (9/16) + (5/2) (x - 3/4)² = 49/16 x - 3/4 = ±7/4 x = 3/4 ± 7/4 x = 5/2 or x = -1
Method 3: Quadratic Formula
- Substitute a = 2, b = -3, and c = -5 into the formula:
x = (-(-3) ± √((-3)² - 4(2)(-5))) / (2(2)) x = (3 ± √49) / 4 x = (3 ± 7) / 4 x = 5/2 or x = -1
Choosing the Best Method:
- Factoring is often the quickest method if it's possible.
- Completing the square is useful when the quadratic equation is not easily factored.
- The quadratic formula is always applicable, even if factoring or completing the square is difficult.
I hope this explanation helps! Feel free to ask if you have any more questions.


Search
Categories
- Technology
- Education
- Business
- Music
- Got talent
- Film
- Politics
- Food
- Games
- Gardening
- Health
- Home
- Literature
- Networking
- Other
- Party
- Religion
- Shopping
- Sports
- Theater
- Wellness
Read More
CAPILLARITY
How does capillary action work in plants?
Capillary action in plants works through the...
Understanding the MOD Function
The MOD function in Excel is used to find the remainder after a number is divided by a divisor....
Black Codes and Segregation in Reconstruction
Black Codes:
The Black Codes were a series of laws passed by Southern states after the Civil...
UACE MATHS 1 WAKISSHA MARKING GUIDE
UACE MATHS 1 WAKISSHA MARKING GUIDE



